Note
Generating spatial weights#
momepy is using libpysal to handle spatial weights, but also builds on top of it. This notebook will show how to use different weights.
[1]:
import momepy
import geopandas as gpd
import matplotlib.pyplot as plt
We will again use osmnx to get the data for our example and after preprocessing of building layer will generate tessellation layer.
[2]:
import osmnx as ox
gdf = ox.geometries.geometries_from_place('Kahla, Germany', tags={'building':True})
buildings = ox.projection.project_gdf(gdf)
buildings['uID'] = momepy.unique_id(buildings)
limit = momepy.buffered_limit(buildings)
tessellation = momepy.Tessellation(buildings, unique_id='uID', limit=limit).tessellation
Inward offset...
Generating input point array...
Generating Voronoi diagram...
Generating GeoDataFrame...
Dissolving Voronoi polygons...
/Users/martin/Git/geopandas/geopandas/geoseries.py:190: DeprecationWarning: The default dtype for empty Series will be 'object' instead of 'float64' in a future version. Specify a dtype explicitly to silence this warning.
s = pd.Series(data, index=index, name=name, **kwargs)
Queen contiguity#
Morphological tessellation allows using contiguity-based weights matrix. While libpysal.weights.contiguity.Queen will do the standard Queen contiguity matrix of the first order; it might not be enough to capture proper context. For that reason, we can use momepy.sw_high to capture all neighbours within set topological distance k. It generates spatial weights of higher orders under the hood and joins them together.
[3]:
sw3 = momepy.sw_high(k=3, gdf=tessellation, ids='uID')
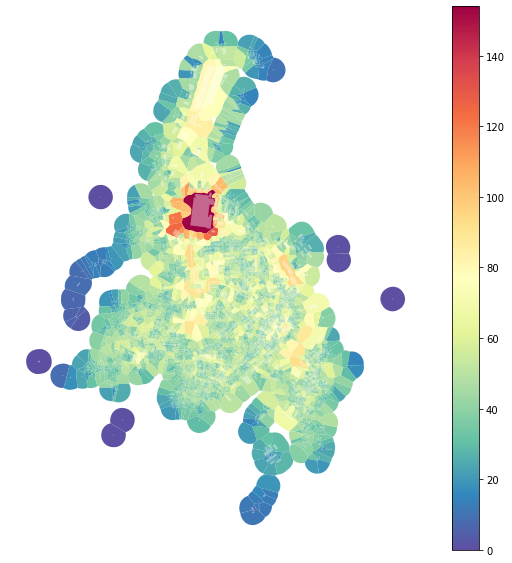
Queen contiguity of morphological tessellation can capture the comparable level of information across the study area - the number of the neighbour is relatively similar and depends on the morphology of urban form. We can visualize it by counting the number of neighbours (as captured by sw3).
[4]:
tessellation['neighbours'] = momepy.Neighbors(tessellation, sw3,'uID').series
[5]:
f, ax = plt.subplots(figsize=(10, 10))
tessellation.plot(ax=ax, column='neighbours', legend=True, cmap='Spectral_r')
buildings.plot(ax=ax, color="white", alpha=0.4)
ax.set_axis_off()
plt.show()
Distance#
Often we want to define the neighbours based on metric distance. We will look at two options - distance band and k-nearest neighbour.
Distance band#
We can imagine distance band as a buffer of a set radius around centroid of each object, for example, 400 meters. For that, we can use libpysal.weights.DistanceBand:
[6]:
import libpysal
dist400 = libpysal.weights.DistanceBand.from_dataframe(buildings, 400,
ids='uID')
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/libpysal/weights/weights.py:172: UserWarning: The weights matrix is not fully connected:
There are 2 disconnected components.
There is 1 island with id: 330.
warnings.warn(message)
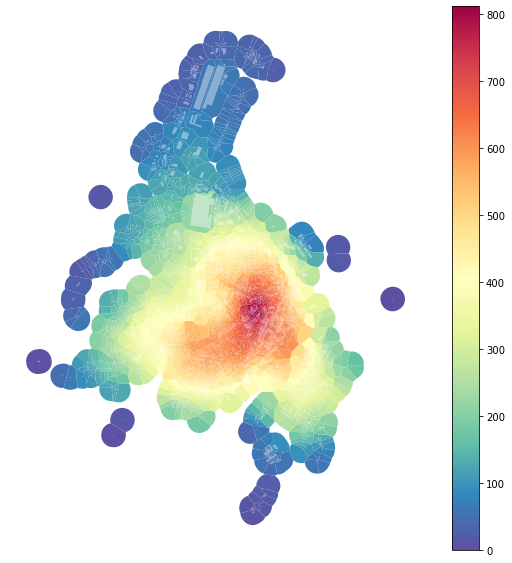
Because we have defined spatial weights using uID, we can use dist400 generated on buildings and use it on tessellation:
[7]:
tessellation['neighbours400'] = momepy.Neighbors(tessellation, dist400, 'uID').series
[8]:
f, ax = plt.subplots(figsize=(10, 10))
tessellation.plot(ax=ax, column='neighbours400', legend=True, cmap='Spectral_r')
buildings.plot(ax=ax, color="white", alpha=0.4)
ax.set_axis_off()
plt.show()
K nearest neighbor#
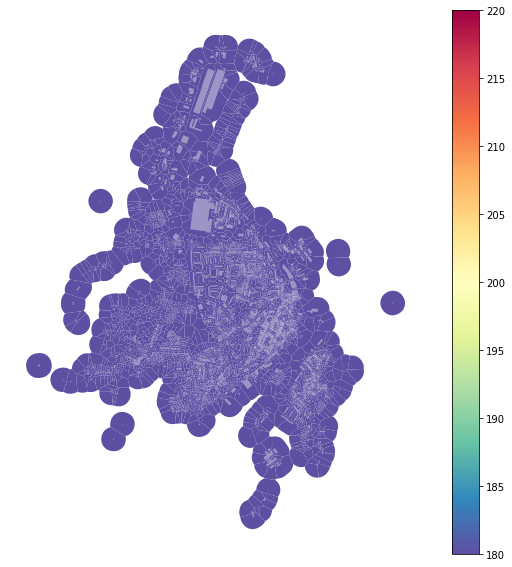
If we want fixed number of neighbours, we can use libpysal.weights.KNN:
[9]:
knn = libpysal.weights.KNN.from_dataframe(buildings, k=200, ids='uID')
tessellation['neighboursKNN'] = momepy.Neighbors(tessellation, knn,'uID').series
Note: As all tessellation cells have the same number of neighbours (due to KNN), they all have the same colour.
[10]:
f, ax = plt.subplots(figsize=(10, 10))
tessellation.plot(ax=ax, column='neighboursKNN', legend=True, cmap='Spectral_r')
buildings.plot(ax=ax, color="white", alpha=0.4)
ax.set_axis_off()
plt.show()
All of them can be used within morphometric analysis. Theoretical and practical differences are discussed in Fleischmann, Romice and Porta (2019).
For the other options on generating spatial weights see lipysal API.