Note
Examples of usage#
Spatial weights are used across momepy. This notebook will illustrate its use on three examples.
[1]:
import momepy
import geopandas as gpd
import matplotlib.pyplot as plt
We will again use osmnx to get the data for our example and after preprocessing of building layer will generate tessellation layer.
[2]:
import osmnx as ox
gdf = ox.geometries.geometries_from_place('Kahla, Germany', tags={'building':True})
buildings = ox.projection.project_gdf(gdf)
buildings['uID'] = momepy.unique_id(buildings)
limit = momepy.buffered_limit(buildings)
tessellation = momepy.Tessellation(buildings, unique_id='uID', limit=limit).tessellation
Inward offset...
Generating input point array...
Generating Voronoi diagram...
Generating GeoDataFrame...
Dissolving Voronoi polygons...
/Users/martin/Git/geopandas/geopandas/geoseries.py:190: DeprecationWarning: The default dtype for empty Series will be 'object' instead of 'float64' in a future version. Specify a dtype explicitly to silence this warning.
s = pd.Series(data, index=index, name=name, **kwargs)
First order contiguity#
Distance to neighbours#
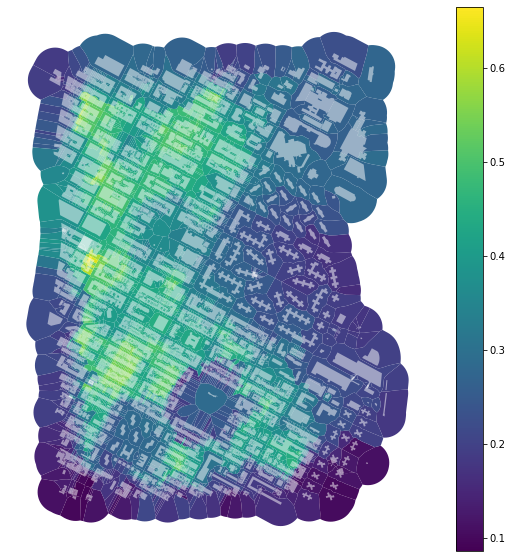
To calculate the mean distance to neighbouring buildings, we need queen contiguity weights of the first order capturing the relationship between immediate neighbours. Relationship between buildings is here represented by relationships between their tessellation cells.
[3]:
sw1 = momepy.sw_high(k=1, gdf=tessellation, ids='uID')
[4]:
buildings['neighbour_dist'] = momepy.NeighborDistance(buildings, sw1, 'uID').series
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pygeos/measurement.py:70: RuntimeWarning: overflow encountered in distance
return lib.distance(a, b, **kwargs)
Note: If there is no neighbour for a building denoted in spatial_weights, the value is set to np.nan. In GeoPandas older than 0.7.0, rows with NaN have to be removed before plotting with natural breaks scheme.
[5]:
buildings = buildings.dropna(subset=['neighbour_dist'])
[6]:
f, ax = plt.subplots(figsize=(10, 10))
buildings.plot(ax=ax, column='neighbour_dist', scheme='naturalbreaks', k=15, legend=True, cmap='Spectral')
ax.set_axis_off()
plt.show()
Higher order / distance#
However, typical usage of spatial weights is to capture the vicinity of each feature. As illustrated in the previous notebook, there are multiple options on how to capture it. In this example, we will use queen contiguity of the higher order (3) based on morphological tessellation.
[7]:
sw3 = momepy.sw_high(k=3, gdf=tessellation, ids='uID')
Average character#
Mean value of selected character within a vicinity of each cell (or building, plot) is a simple example. AverageCharacter can measure mean, median or mode and defaults to all. Each of them can be accessed using .mean, .median or .mode. .series will return mean.
[8]:
areas = momepy.Area(tessellation).series
mean_area = momepy.AverageCharacter(
tessellation, values=areas, spatial_weights=sw3, unique_id='uID')
tessellation['mean_area'] = mean_area.mean
[9]:
f, ax = plt.subplots(figsize=(10, 10))
tessellation.plot(ax=ax, column='mean_area', legend=True, scheme='quantiles', k=15, cmap='Blues_r')
buildings.plot(ax=ax, color="white", alpha=0.4)
ax.set_axis_off()
plt.show()
In some cases, we might want to eliminate the effect of outliers. To do so, we can specify the range on which should AverageCharacter calculate mean. Below we will measure only interquartile mean.
[10]:
tessellation['mean_area_iq'] = momepy.AverageCharacter(
tessellation, areas, sw3, 'uID', rng=(25, 75)).mean
[11]:
f, ax = plt.subplots(figsize=(10, 10))
tessellation.plot(ax=ax, column='mean_area_iq', legend=True, scheme='quantiles', k=15, cmap='Greens_r')
buildings.plot(ax=ax, color="white", alpha=0.4)
ax.set_axis_off()
plt.show()
Another option would be to calculate median only:
[12]:
tessellation['med_area'] = momepy.AverageCharacter(
tessellation, areas, sw3, 'uID', mode='median').median
[13]:
f, ax = plt.subplots(figsize=(10, 10))
tessellation.plot(ax=ax, column='med_area', legend=True, scheme='quantiles', k=15, cmap='Purples_r')
buildings.plot(ax=ax, color="white", alpha=0.4)
ax.set_axis_off()
plt.show()

Weighted character#
The weighted average is another example using the same spatial weights. For illustration, we can try area-weighted circular compactness:
[14]:
circular_compactness = momepy.CircularCompactness(buildings)
buildings['weighted_circom'] = momepy.WeightedCharacter(
buildings, circular_compactness.series, sw3, 'uID', momepy.Area(buildings).series).series
[15]:
f, ax = plt.subplots(figsize=(10, 10))
buildings.plot(ax=ax, column='weighted_circom', legend=True, scheme='quantiles', k=15, cmap='viridis')
ax.set_axis_off()
plt.show()
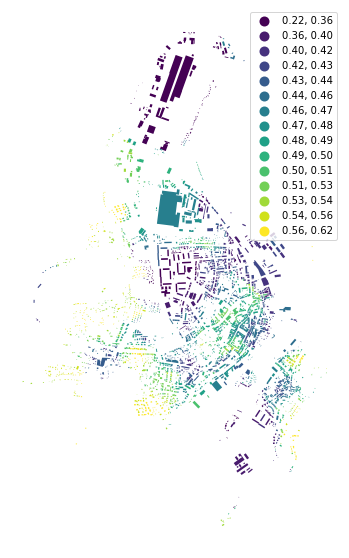
Density#
We will again use our Manhattan case study to illustrate Density.
[16]:
point = (40.731603, -73.977857)
dist = 1000
gdf = ox.geometries.geometries_from_point(point, dist=dist, tags={'building':True})
gdf_projected = ox.projection.project_gdf(gdf)
buildings = gdf_projected[gdf_projected.geom_type.isin(['Polygon', 'MultiPolygon'])]
buildings['uID'] = momepy.unique_id(buildings)
limit = momepy.buffered_limit(buildings)
tessellation = momepy.Tessellation(buildings, unique_id='uID', limit=limit).tessellation
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pandas/core/frame.py:3607: SettingWithCopyWarning:
A value is trying to be set on a copy of a slice from a DataFrame.
Try using .loc[row_indexer,col_indexer] = value instead
See the caveats in the documentation: https://pandas.pydata.org/pandas-docs/stable/user_guide/indexing.html#returning-a-view-versus-a-copy
self._set_item(key, value)
Inward offset...
Generating input point array...
Generating Voronoi diagram...
Generating GeoDataFrame...
Dissolving Voronoi polygons...
/Users/martin/Git/geopandas/geopandas/geoseries.py:190: DeprecationWarning: The default dtype for empty Series will be 'object' instead of 'float64' in a future version. Specify a dtype explicitly to silence this warning.
s = pd.Series(data, index=index, name=name, **kwargs)
/Users/martin/Git/momepy/momepy/elements.py:386: UserWarning: Tessellation contains MultiPolygon elements. Initial objects should be edited. unique_id of affected elements: [217, 405, 833, 835, 1994, 3053, 3056, 3070, 3136, 3147, 3157, 3163]
warnings.warn(
[17]:
f, ax = plt.subplots(figsize=(10, 10))
tessellation.plot(ax=ax)
buildings.plot(ax=ax, color='white', alpha=.5)
ax.set_axis_off()
plt.show()

To get gross density, we need to know floor areas:
[18]:
def clean_heights(x):
try:
return float(x)
except ValueError:
return 0
buildings['height'] = buildings['height'].fillna(0).apply(clean_heights)
buildings['floor_area'] = momepy.FloorArea(buildings, 'height').series
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pandas/core/frame.py:3607: SettingWithCopyWarning:
A value is trying to be set on a copy of a slice from a DataFrame.
Try using .loc[row_indexer,col_indexer] = value instead
See the caveats in the documentation: https://pandas.pydata.org/pandas-docs/stable/user_guide/indexing.html#returning-a-view-versus-a-copy
self._set_item(key, value)
Now we merge floor areas to tessellation based on shared unique ID and generate spatial weights.
[19]:
tessellation = tessellation.merge(buildings[['uID', 'floor_area']])
sw = momepy.sw_high(k=3, gdf=tessellation, ids='uID')
Density is then following the same principle as illustrated above.
[20]:
gross = momepy.Density(
tessellation, values='floor_area', spatial_weights=sw, unique_id='uID')
tessellation['gross_density'] = gross.series
[21]:
f, ax = plt.subplots(figsize=(10, 10))
tessellation.plot(ax=ax, column='gross_density', legend=True, scheme='naturalbreaks', k=15)
buildings.plot(ax=ax, color='white', alpha=.5)
ax.set_axis_off()
plt.show()
In a similar way can be done gross coverage.
[22]:
buildings['area'] = momepy.Area(buildings).series
tessellation = tessellation.merge(buildings[['uID', 'area']])
/opt/miniconda3/envs/geo_dev/lib/python3.9/site-packages/pandas/core/frame.py:3607: SettingWithCopyWarning:
A value is trying to be set on a copy of a slice from a DataFrame.
Try using .loc[row_indexer,col_indexer] = value instead
See the caveats in the documentation: https://pandas.pydata.org/pandas-docs/stable/user_guide/indexing.html#returning-a-view-versus-a-copy
self._set_item(key, value)
[23]:
coverage = momepy.Density(
tessellation, values='area', spatial_weights=sw, unique_id='uID')
tessellation['gross_coverage'] = coverage.series
[24]:
f, ax = plt.subplots(figsize=(10, 10))
tessellation.plot(ax=ax, column='gross_coverage', legend=True)
buildings.plot(ax=ax, color='white', alpha=.5)
ax.set_axis_off()
plt.show()