Note
Simplified detection of urban types#
Example adapted from the SDSC 2021 Workshop led by Martin Fleischmann. You can see the recording of the workshop on YouTube.
This example illustrates the potential of morphometrics captured by momepy in capturing the structure of cities. We will pick a town, fetch its data from the OpenStreetMap, and analyse it to detect individual types of urban structure within it.
This method is only illustrative and is based on the more extensive one published by Fleischmann et al. (2021) available from martinfleis/numerical-taxonomy-paper.
Fleischmann M, Feliciotti A, Romice O and Porta S (2021) Methodological Foundation of a Numerical Taxonomy of Urban Form. Environment and Planning B: Urban Analytics and City Science, doi: 10.1177/23998083211059835
It depends on the following packages:
- momepy
- osmnx
- clustergram
- bokeh
- scikit-learn
- geopy
- ipywidgets
[1]:
import geopandas
import libpysal
import momepy
import osmnx
import pandas
from clustergram import Clustergram
import matplotlib.pyplot as plt
from bokeh.io import output_notebook
from bokeh.plotting import show
output_notebook()
Pick a place, ideally a town with a good coverage in OpenStreetMap and its local CRS.
[2]:
place = 'Znojmo, Czechia'
local_crs = 5514
We can interactively explore the place we just selected.
[3]:
geopandas.tools.geocode(place).explore()
[3]:
Input data#
We can use OSMnx to quickly download data from OpenStreetMap. If you intend to download larger areas, we recommend using pyrosm instead.
Buildings#
[4]:
buildings = osmnx.features_from_place(place, tags={'building':True})
buildings.head()
[4]:
| power | geometry | amenity | brand | brand:wikidata | brand:wikipedia | check_date | name | operator | operator:wikidata | ... | material | name:signed | ref | monitoring:water_level | takeaway | shelter_type | construction | ways | type | emergency | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| element_type | osmid | |||||||||||||||||||||
| node | 3372076291 | NaN | POINT (16.05376 48.84683) | NaN | NaN | NaN | NaN | NaN | 7/I/10/A-120 | NaN | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 3372076393 | NaN | POINT (16.05581 48.84158) | NaN | NaN | NaN | NaN | NaN | 7/I/11/A-140 Z | NaN | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | |
| 3372076394 | NaN | POINT (16.05867 48.83522) | NaN | NaN | NaN | NaN | NaN | 7/I/12/A-220 | NaN | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | |
| 3372076428 | NaN | POINT (16.03949 48.85599) | NaN | NaN | NaN | NaN | NaN | 7/I/8/E | NaN | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | |
| 3372076429 | NaN | POINT (16.04133 48.85501) | NaN | NaN | NaN | NaN | NaN | 7/I/9/E | NaN | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
5 rows × 119 columns
The OSM input may need a bit of cleaning to ensure only proper polygons are kept.
[5]:
buildings.geom_type.value_counts()
[5]:
Polygon 12214
Point 7
Name: count, dtype: int64
[6]:
buildings = buildings[buildings.geom_type == "Polygon"].reset_index(drop=True)
And we should re-project the data from WGS84 to the local projection in meters (momepy default values assume meters not feet or degrees). We will also drop unnecessary columns.
[7]:
buildings = buildings[["geometry"]].to_crs(local_crs)
Finally, we can assign unique ID to each row.
[8]:
buildings["uID"] = range(len(buildings))
buildings.head()
[8]:
| geometry | uID | |
|---|---|---|
| 0 | POLYGON ((-643743.474 -1193358.749, -643743.30... | 0 |
| 1 | POLYGON ((-643751.446 -1193530.633, -643749.37... | 1 |
| 2 | POLYGON ((-643281.601 -1193130.831, -643283.76... | 2 |
| 3 | POLYGON ((-643381.904 -1193174.697, -643388.48... | 3 |
| 4 | POLYGON ((-643370.450 -1193130.215, -643398.26... | 4 |
Streets#
Similar operations are done with streets.
[9]:
osm_graph = osmnx.graph_from_place(place, network_type='drive')
osm_graph = osmnx.projection.project_graph(osm_graph, to_crs=local_crs)
streets = osmnx.graph_to_gdfs(
osm_graph,
nodes=False,
edges=True,
node_geometry=False,
fill_edge_geometry=True
)
[10]:
streets.head()
[10]:
| osmid | ref | name | highway | maxspeed | oneway | reversed | length | geometry | lanes | bridge | junction | width | tunnel | access | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| u | v | key | |||||||||||||||
| 74103628 | 639231391 | 0 | 33733060 | 361 | Přímětická | secondary | 50 | False | False | 24.574 | LINESTRING (-643239.057 -1192850.232, -643229.... | NaN | NaN | NaN | NaN | NaN | NaN |
| 3775990798 | 0 | 33733060 | 361 | Přímětická | secondary | 50 | False | True | 60.354 | LINESTRING (-643239.057 -1192850.232, -643241.... | NaN | NaN | NaN | NaN | NaN | NaN | |
| 639231391 | 74103628 | 0 | 33733060 | 361 | Přímětická | secondary | 50 | False | True | 24.574 | LINESTRING (-643229.639 -1192872.949, -643239.... | NaN | NaN | NaN | NaN | NaN | NaN |
| 74142638 | 0 | 33733060 | 361 | Přímětická | secondary | 50 | False | False | 54.260 | LINESTRING (-643229.639 -1192872.949, -643219.... | NaN | NaN | NaN | NaN | NaN | NaN | |
| 639231314 | 0 | 50313241 | NaN | Mičurinova | residential | NaN | True | False | 101.376 | LINESTRING (-643229.639 -1192872.949, -643233.... | NaN | NaN | NaN | NaN | NaN | NaN |
We can also do some preprocessing using momepy to ensure we have proper network topology.
[11]:
streets = momepy.remove_false_nodes(streets)
streets = streets[["geometry"]]
streets["nID"] = range(len(streets))
/Users/martin/miniforge3/envs/stable/lib/python3.12/site-packages/geopandas/array.py:1459: UserWarning: CRS not set for some of the concatenation inputs. Setting output's CRS as S-JTSK / Krovak East North (the single non-null crs provided).
return GeometryArray(data, crs=_get_common_crs(to_concat))
[12]:
streets.head()
[12]:
| geometry | nID | |
|---|---|---|
| 0 | LINESTRING (-643239.057 -1192850.232, -643229.... | 0 |
| 1 | LINESTRING (-643239.057 -1192850.232, -643241.... | 1 |
| 2 | LINESTRING (-643229.639 -1192872.949, -643239.... | 2 |
| 3 | LINESTRING (-643229.639 -1192872.949, -643219.... | 3 |
| 4 | LINESTRING (-643229.639 -1192872.949, -643233.... | 4 |
Generated data#
Tessellation#
Given building footprints:

We can generate a spatial unit using morphological tessellation:

[13]:
limit = momepy.buffered_limit(buildings, 100)
tessellation = momepy.Tessellation(buildings, "uID", limit, verbose=False, segment=1)
tessellation = tessellation.tessellation
/var/folders/2f/fhks6w_d0k556plcv3rfmshw0000gn/T/ipykernel_84424/1328706492.py:3: UserWarning: Tessellation does not fully match buildings. 20 element(s) collapsed during generation - unique_id: {3968, 4227, 11255, 10686, 10687, 9026, 4177, 11473, 11474, 8534, 11478, 4185, 4188, 10465, 9061, 3958, 4215, 4218, 4222, 4223}.
tessellation = momepy.Tessellation(buildings, "uID", limit, verbose=False, segment=1)
/var/folders/2f/fhks6w_d0k556plcv3rfmshw0000gn/T/ipykernel_84424/1328706492.py:3: UserWarning: Tessellation contains MultiPolygon elements. Initial objects should be edited. `unique_id` of affected elements: [4167, 3227, 11783, 3173, 10997].
tessellation = momepy.Tessellation(buildings, "uID", limit, verbose=False, segment=1)
Link streets#
Link unique IDs of streets to buildings and tessellation cells based on the nearest neighbor join.
[14]:
buildings = buildings.sjoin_nearest(streets, max_distance=1000, how="left")
buildings.head()
[14]:
| geometry | uID | index_right | nID | |
|---|---|---|---|---|
| 0 | POLYGON ((-643743.474 -1193358.749, -643743.30... | 0 | 1047.0 | 1047.0 |
| 0 | POLYGON ((-643743.474 -1193358.749, -643743.30... | 0 | 1048.0 | 1048.0 |
| 1 | POLYGON ((-643751.446 -1193530.633, -643749.37... | 1 | 1485.0 | 1485.0 |
| 2 | POLYGON ((-643281.601 -1193130.831, -643283.76... | 2 | 243.0 | 243.0 |
| 2 | POLYGON ((-643281.601 -1193130.831, -643283.76... | 2 | 887.0 | 887.0 |
Clean duplicates and attach the network ID to the tessellation as well.
[15]:
buildings = buildings.drop_duplicates("uID").drop(columns="index_right")
tessellation = tessellation.merge(buildings[['uID', 'nID']], on='uID', how='left')
Measure#
Measure individual morphometric characters. For details see the User Guide and the API reference.
Dimensions#
[16]:
buildings["area"] = buildings.area
tessellation["area"] = tessellation.area
streets["length"] = streets.length
Shape#
[17]:
buildings['eri'] = momepy.EquivalentRectangularIndex(buildings).series
buildings['elongation'] = momepy.Elongation(buildings).series
tessellation['convexity'] = momepy.Convexity(tessellation).series
streets["linearity"] = momepy.Linearity(streets).series
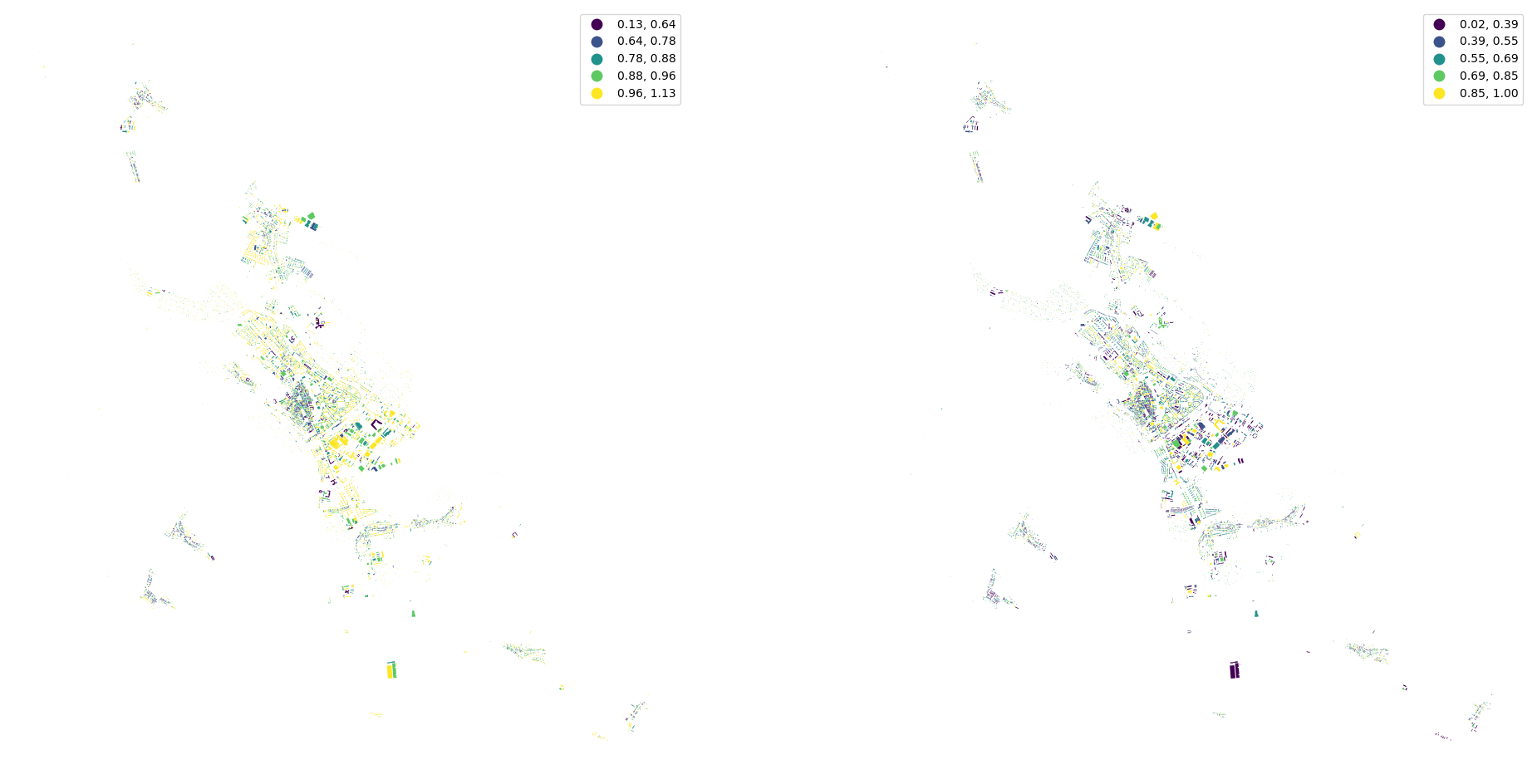
[18]:
fig, ax = plt.subplots(1, 2, figsize=(24, 12))
buildings.plot("eri", ax=ax[0], scheme="natural_breaks", legend=True)
buildings.plot("elongation", ax=ax[1], scheme="natural_breaks", legend=True)
ax[0].set_axis_off()
ax[1].set_axis_off()
[19]:
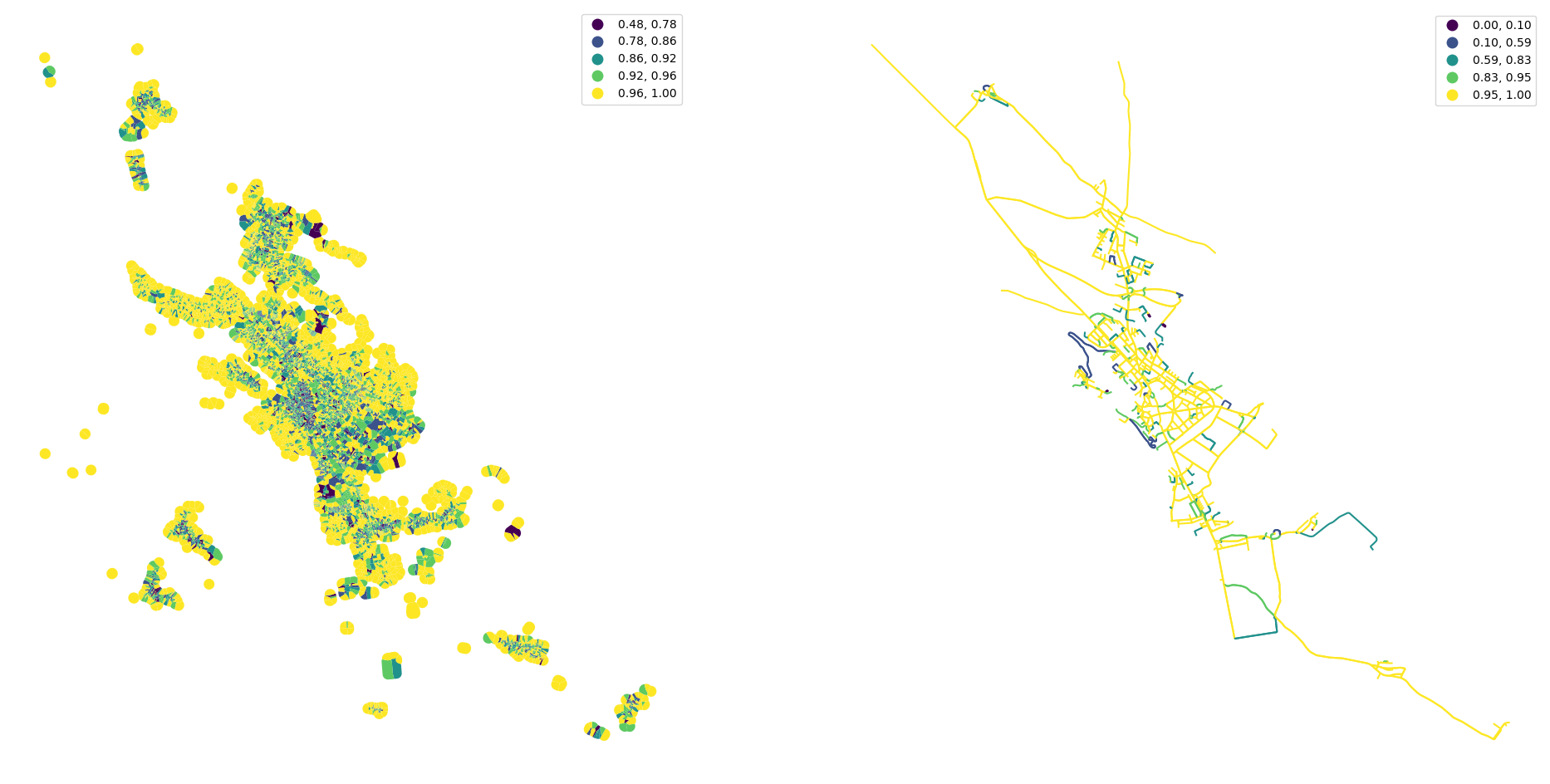
fig, ax = plt.subplots(1, 2, figsize=(24, 12))
tessellation.plot("convexity", ax=ax[0], scheme="natural_breaks", legend=True)
streets.plot("linearity", ax=ax[1], scheme="natural_breaks", legend=True)
ax[0].set_axis_off()
ax[1].set_axis_off()
Spatial distribution#
[20]:
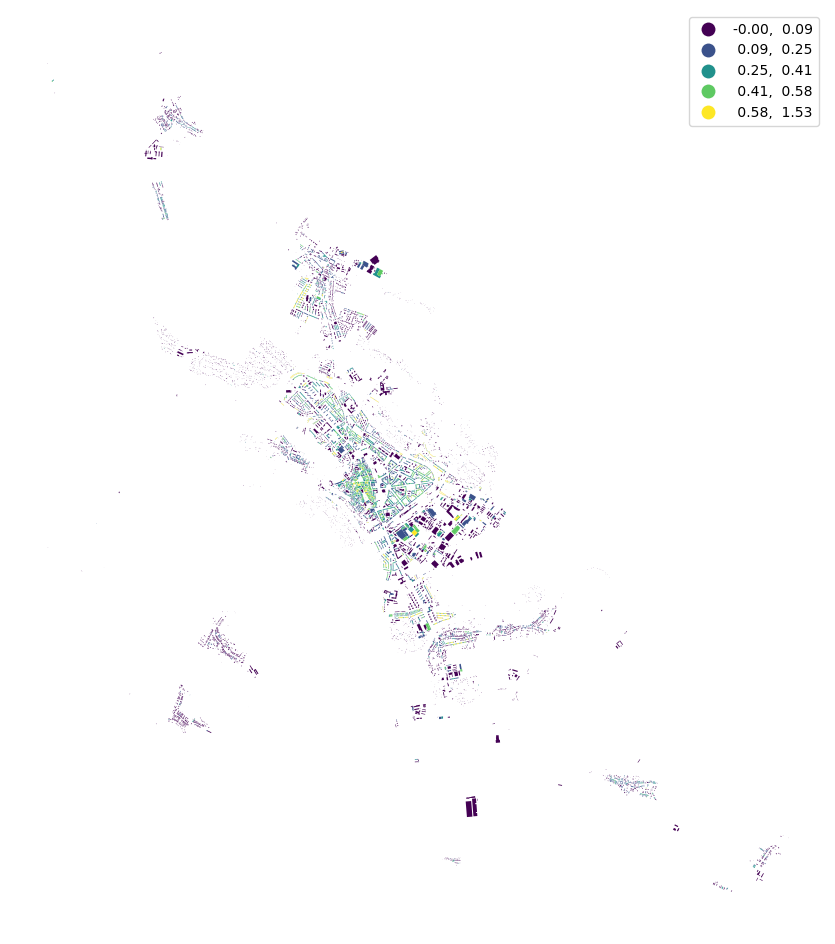
buildings["shared_walls"] = momepy.SharedWallsRatio(buildings).series
buildings.plot("shared_walls", figsize=(12, 12), scheme="natural_breaks", legend=True).set_axis_off()
/Users/martin/miniforge3/envs/stable/lib/python3.12/site-packages/momepy/distribution.py:135: FutureWarning: The `query_bulk()` method is deprecated and will be removed in GeoPandas 1.0. You can use the `query()` method instead.
inp, res = gdf.sindex.query_bulk(gdf.geometry, predicate="intersects")
/Users/martin/miniforge3/envs/stable/lib/python3.12/site-packages/shapely/set_operations.py:131: RuntimeWarning: invalid value encountered in intersection
return lib.intersection(a, b, **kwargs)
Generate spatial weights matrix using libpysal.
[21]:
queen_1 = libpysal.weights.contiguity.Queen.from_dataframe(tessellation, ids="uID", silence_warnings=True)
[22]:
tessellation["neighbors"] = momepy.Neighbors(tessellation, queen_1, "uID", weighted=True, verbose=False).series
tessellation["covered_area"] = momepy.CoveredArea(tessellation, queen_1, "uID", verbose=False).series
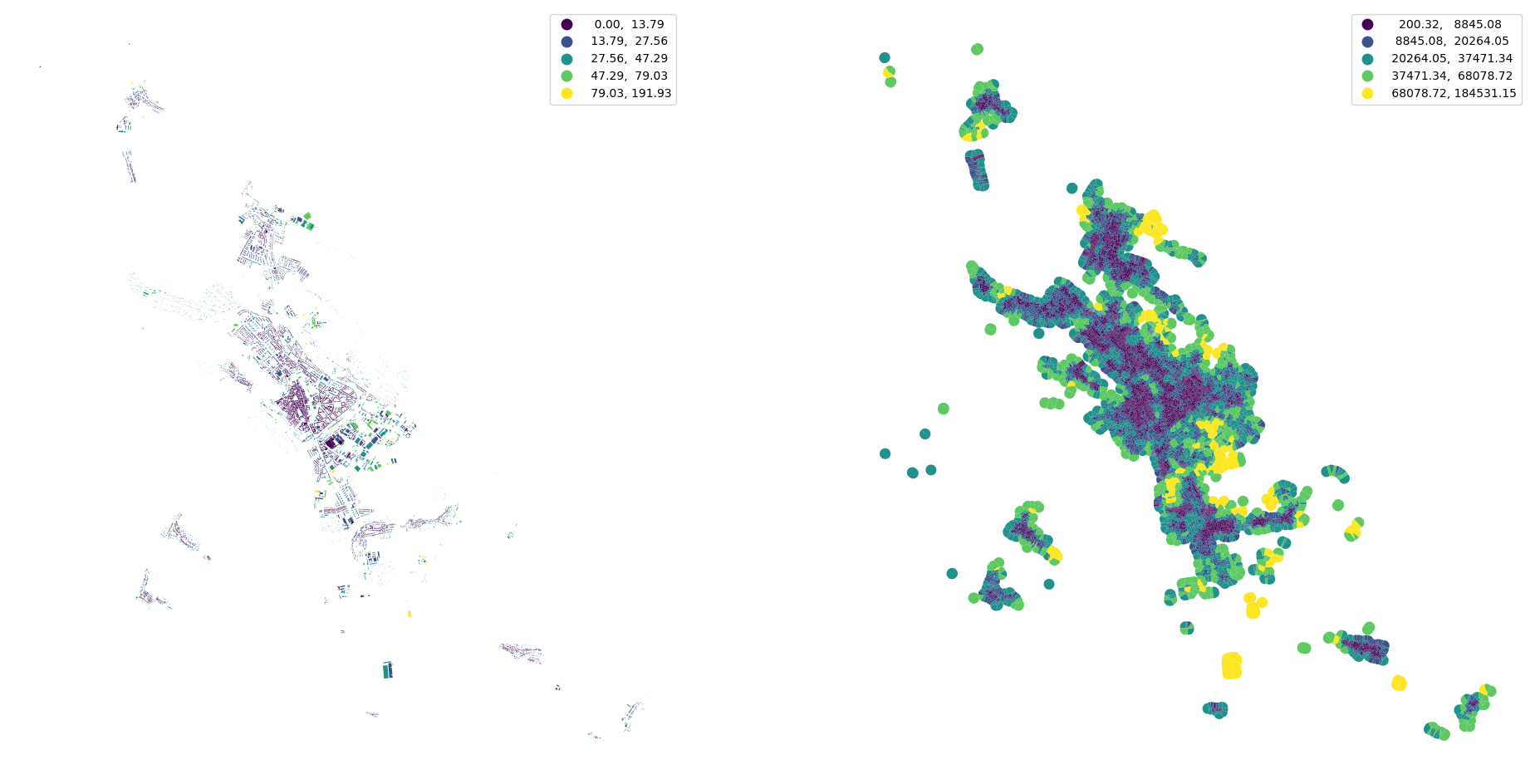
buildings["neighbor_distance"] = momepy.NeighborDistance(buildings, queen_1, "uID", verbose=False).series
[23]:
fig, ax = plt.subplots(1, 2, figsize=(24, 12))
buildings.plot("neighbor_distance", ax=ax[0], scheme="natural_breaks", legend=True)
tessellation.plot("covered_area", ax=ax[1], scheme="natural_breaks", legend=True)
ax[0].set_axis_off()
ax[1].set_axis_off()
[24]:
queen_3 = momepy.sw_high(k=3, weights=queen_1)
buildings_q1 = libpysal.weights.contiguity.Queen.from_dataframe(buildings, silence_warnings=True)
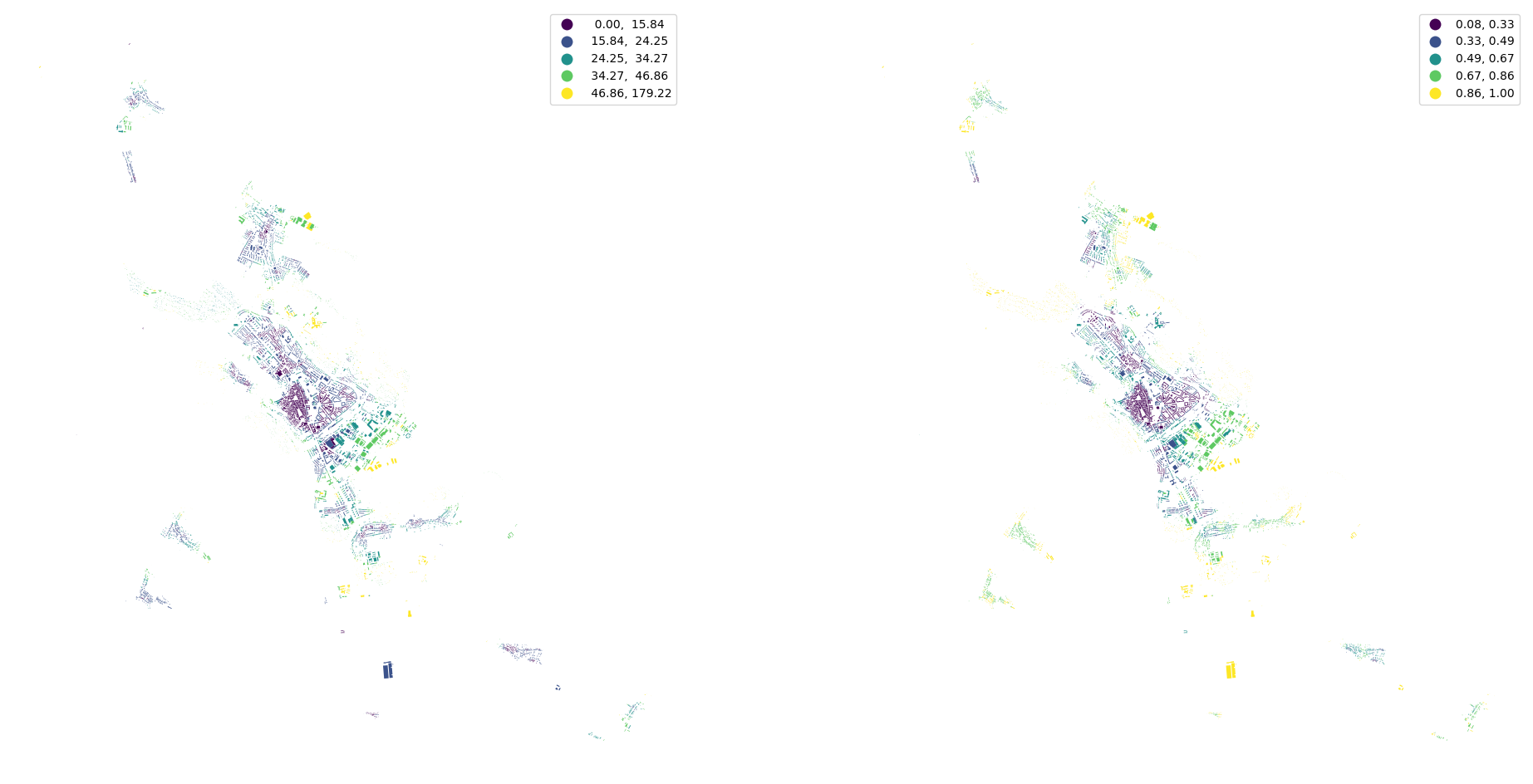
buildings['interbuilding_distance'] = momepy.MeanInterbuildingDistance(buildings, queen_1, 'uID', 3, verbose=False).series
buildings['adjacency'] = momepy.BuildingAdjacency(buildings, queen_3, 'uID', buildings_q1, verbose=False).series
/var/folders/2f/fhks6w_d0k556plcv3rfmshw0000gn/T/ipykernel_84424/738459904.py:2: FutureWarning: `use_index` defaults to False but will default to True in future. Set True/False directly to control this behavior and silence this warning
buildings_q1 = libpysal.weights.contiguity.Queen.from_dataframe(buildings, silence_warnings=True)
[25]:
fig, ax = plt.subplots(1, 2, figsize=(24, 12))
buildings.plot("interbuilding_distance", ax=ax[0], scheme="natural_breaks", legend=True)
buildings.plot("adjacency", ax=ax[1], scheme="natural_breaks", legend=True)
ax[0].set_axis_off()
ax[1].set_axis_off()
[26]:
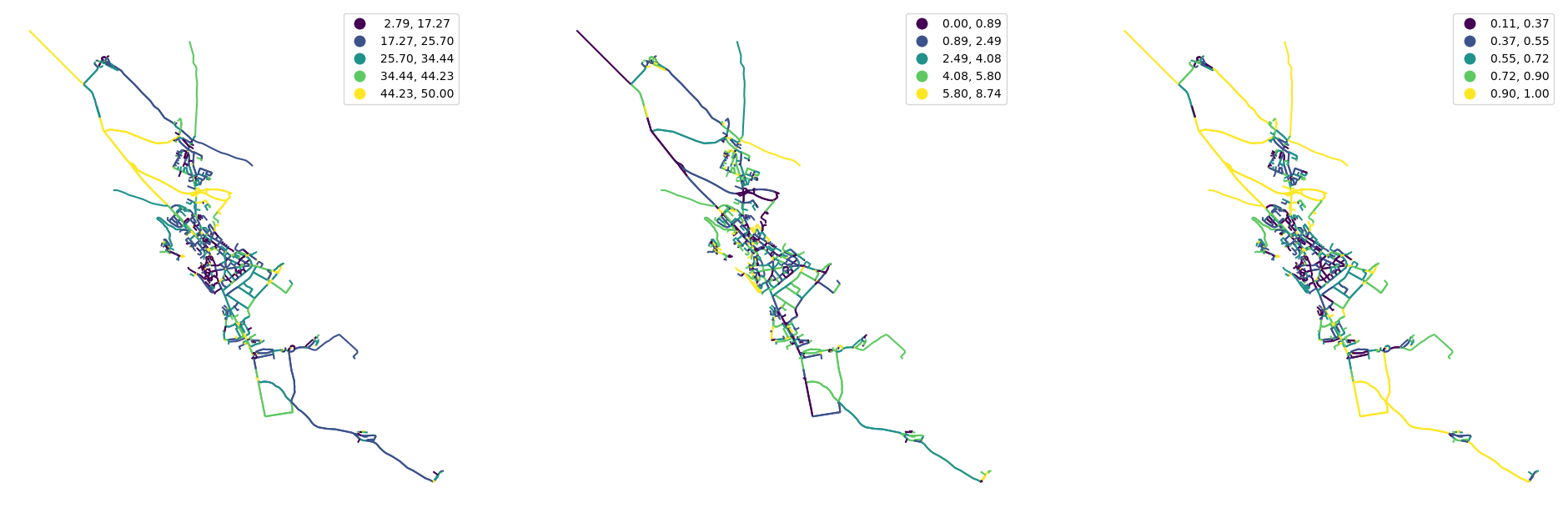
profile = momepy.StreetProfile(streets, buildings)
streets["width"] = profile.w
streets["width_deviation"] = profile.wd
streets["openness"] = profile.o
[27]:
fig, ax = plt.subplots(1, 3, figsize=(24, 12))
streets.plot("width", ax=ax[0], scheme="natural_breaks", legend=True)
streets.plot("width_deviation", ax=ax[1], scheme="natural_breaks", legend=True)
streets.plot("openness", ax=ax[2], scheme="natural_breaks", legend=True)
ax[0].set_axis_off()
ax[1].set_axis_off()
ax[2].set_axis_off()
Intensity#
[28]:
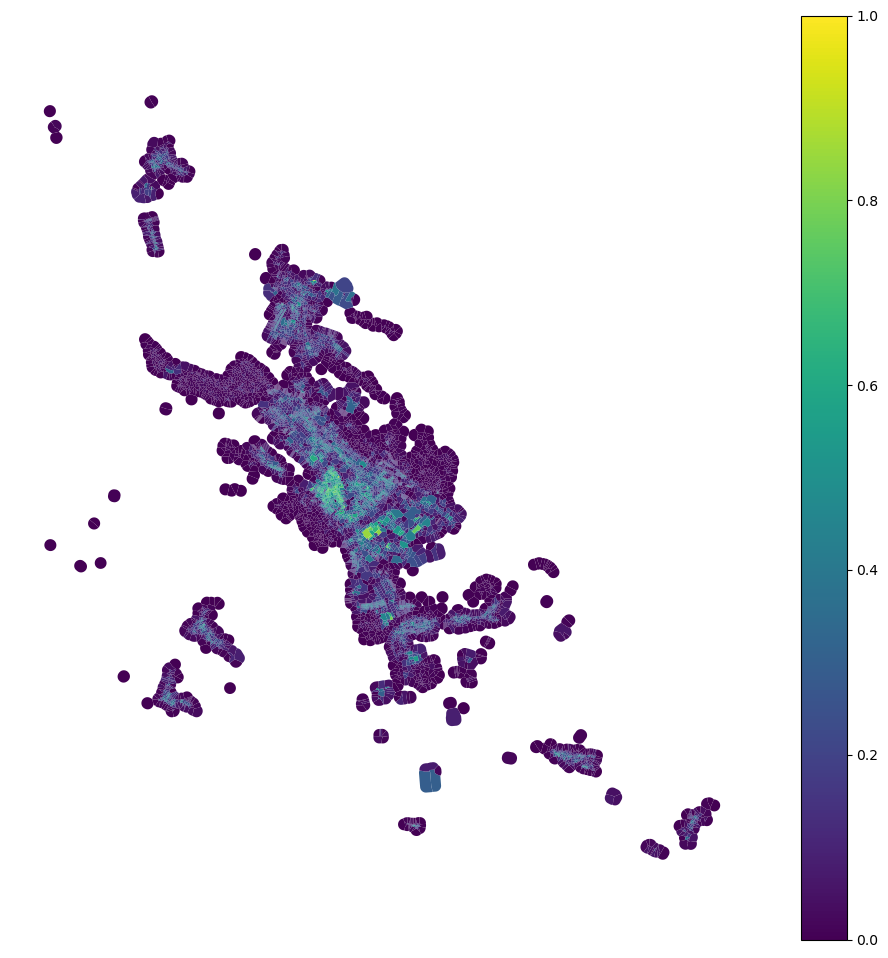
tessellation['car'] = momepy.AreaRatio(tessellation, buildings, 'area', 'area', 'uID').series
tessellation.plot("car", figsize=(12, 12), vmin=0, vmax=1, legend=True).set_axis_off()
Connectivity#
[29]:
graph = momepy.gdf_to_nx(streets)
graph = momepy.node_degree(graph)
graph = momepy.closeness_centrality(graph, radius=400, distance="mm_len")
graph = momepy.meshedness(graph, radius=400, distance="mm_len")
nodes, streets = momepy.nx_to_gdf(graph)
/Users/martin/miniforge3/envs/stable/lib/python3.12/site-packages/tqdm/std.py:580: DeprecationWarning: datetime.datetime.utcfromtimestamp() is deprecated and scheduled for removal in a future version. Use timezone-aware objects to represent datetimes in UTC: datetime.datetime.fromtimestamp(timestamp, datetime.UTC).
if rate and total else datetime.utcfromtimestamp(0))
[30]:
fig, ax = plt.subplots(1, 3, figsize=(24, 12))
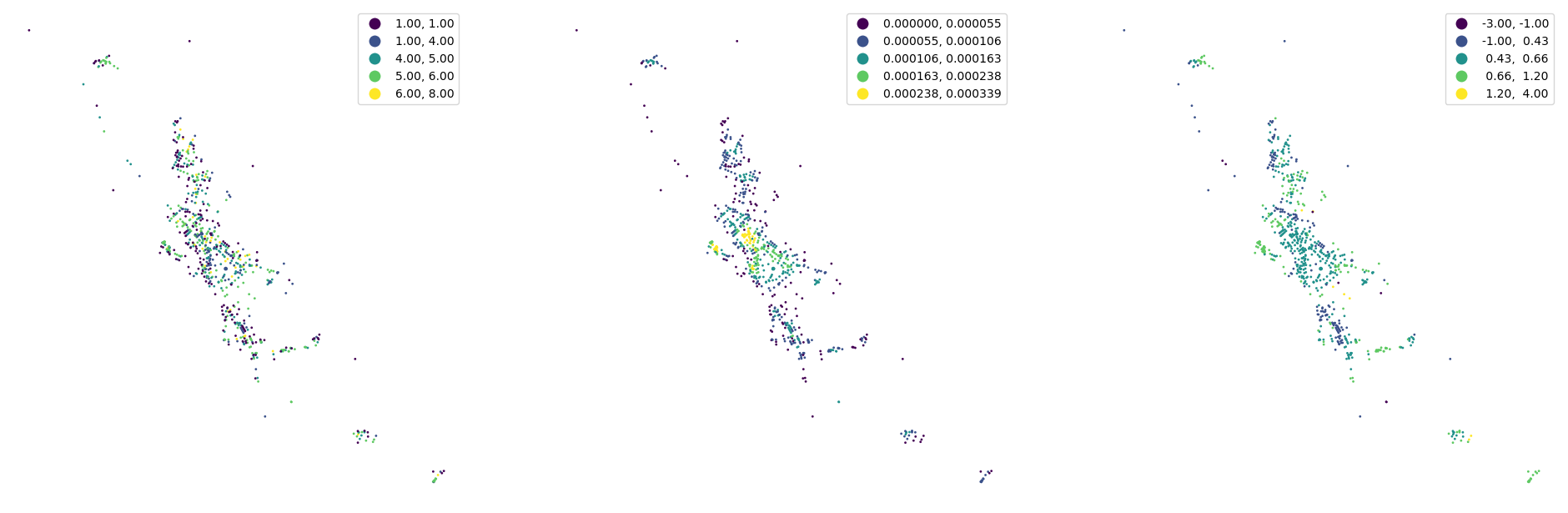
nodes.plot("degree", ax=ax[0], scheme="natural_breaks", legend=True, markersize=1)
nodes.plot("closeness", ax=ax[1], scheme="natural_breaks", legend=True, markersize=1, legend_kwds={"fmt": "{:.6f}"})
nodes.plot("meshedness", ax=ax[2], scheme="natural_breaks", legend=True, markersize=1)
ax[0].set_axis_off()
ax[1].set_axis_off()
ax[2].set_axis_off()
[31]:
buildings["nodeID"] = momepy.get_node_id(buildings, nodes, streets, "nodeID", "nID")
/Users/martin/miniforge3/envs/stable/lib/python3.12/site-packages/tqdm/std.py:580: DeprecationWarning: datetime.datetime.utcfromtimestamp() is deprecated and scheduled for removal in a future version. Use timezone-aware objects to represent datetimes in UTC: datetime.datetime.fromtimestamp(timestamp, datetime.UTC).
if rate and total else datetime.utcfromtimestamp(0))
Link all data together (to tessellation cells or buildings).
[32]:
tessellation.head()
[32]:
| uID | geometry | nID | area | convexity | neighbors | covered_area | car | |
|---|---|---|---|---|---|---|---|---|
| 0 | 5329 | POLYGON ((-637358.313 -1200006.277, -637357.92... | 637.0 | 27736.670898 | 0.995293 | 0.003108 | 41793.250296 | 0.007476 |
| 1 | 5295 | POLYGON ((-636869.686 -1199824.120, -636870.16... | 647.0 | 19855.193192 | 0.942935 | 0.005466 | 59301.601010 | 0.022276 |
| 2 | 10470 | POLYGON ((-637462.192 -1199942.387, -637450.89... | 637.0 | 5980.537479 | 0.900015 | 0.006719 | 23484.755027 | 0.066270 |
| 3 | 5328 | POLYGON ((-636567.904 -1199437.917, -636567.88... | 1636.0 | 17651.421590 | 0.989690 | 0.005897 | 43087.114344 | 0.005919 |
| 4 | 10476 | POLYGON ((-637599.665 -1199909.097, -637595.79... | 637.0 | 6221.647570 | 0.829355 | 0.010157 | 43342.518118 | 0.049808 |
[33]:
merged = tessellation.merge(buildings.drop(columns=['nID', 'geometry']), on='uID')
merged = merged.merge(streets.drop(columns='geometry'), on='nID', how='left')
merged = merged.merge(nodes.drop(columns='geometry'), on='nodeID', how='left')
[34]:
merged.columns
[34]:
Index(['uID', 'geometry', 'nID', 'area_x', 'convexity', 'neighbors',
'covered_area', 'car', 'area_y', 'eri', 'elongation', 'shared_walls',
'neighbor_distance', 'interbuilding_distance', 'adjacency', 'nodeID',
'length', 'linearity', 'width', 'width_deviation', 'openness', 'mm_len',
'node_start', 'node_end', 'degree', 'closeness', 'meshedness'],
dtype='object')
Understanding the context#
Measure first, second and third quartile of distribution of values within an area around each building.
[35]:
percentiles = []
for column in merged.columns.drop(["uID", "nodeID", "nID", 'mm_len', 'node_start', 'node_end', "geometry"]):
perc = momepy.Percentiles(merged, column, queen_3, "uID", verbose=False).frame
perc.columns = [f"{column}_" + str(x) for x in perc.columns]
percentiles.append(perc)
[36]:
percentiles_joined = pandas.concat(percentiles, axis=1)
percentiles_joined.head()
[36]:
| area_x_25 | area_x_50 | area_x_75 | convexity_25 | convexity_50 | convexity_75 | neighbors_25 | neighbors_50 | neighbors_75 | covered_area_25 | ... | openness_75 | degree_25 | degree_50 | degree_75 | closeness_25 | closeness_50 | closeness_75 | meshedness_25 | meshedness_50 | meshedness_75 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 7151.505439 | 8460.534527 | 9102.552267 | 0.874500 | 0.888902 | 0.929755 | 0.006852 | 0.007068 | 0.007307 | 38509.340859 | ... | 0.952261 | 6.0 | 6.0 | 6.0 | 0.000087 | 0.000087 | 0.000087 | 0.894737 | 0.894737 | 0.894737 |
| 1 | 2049.363971 | 4069.346269 | 7207.822493 | 0.934390 | 0.957400 | 0.980033 | 0.015075 | 0.020266 | 0.027499 | 26373.762179 | ... | 1.000000 | 4.0 | 6.0 | 6.0 | 0.000094 | 0.000094 | 0.000099 | 0.809524 | 0.894737 | 1.000000 |
| 2 | 4869.281368 | 6119.443335 | 9102.552267 | 0.874500 | 0.947803 | 0.971754 | 0.007068 | 0.008105 | 0.009836 | 28474.090834 | ... | 0.952261 | 6.0 | 6.0 | 6.0 | 0.000087 | 0.000087 | 0.000087 | 0.894737 | 0.894737 | 0.894737 |
| 3 | 979.082829 | 2497.478414 | 9114.443041 | 0.945396 | 0.976589 | 0.989613 | 0.011906 | 0.027560 | 0.044586 | 8894.839436 | ... | 0.677778 | 1.0 | 4.0 | 7.0 | 0.000049 | 0.000063 | 0.000087 | 0.736842 | 0.809524 | 0.809524 |
| 4 | 5615.435877 | 6119.443335 | 8460.534527 | 0.888902 | 0.947803 | 0.971754 | 0.007598 | 0.008616 | 0.009836 | 27790.702394 | ... | 0.952261 | 6.0 | 6.0 | 6.0 | 0.000087 | 0.000087 | 0.000087 | 0.894737 | 0.894737 | 0.894737 |
5 rows × 60 columns
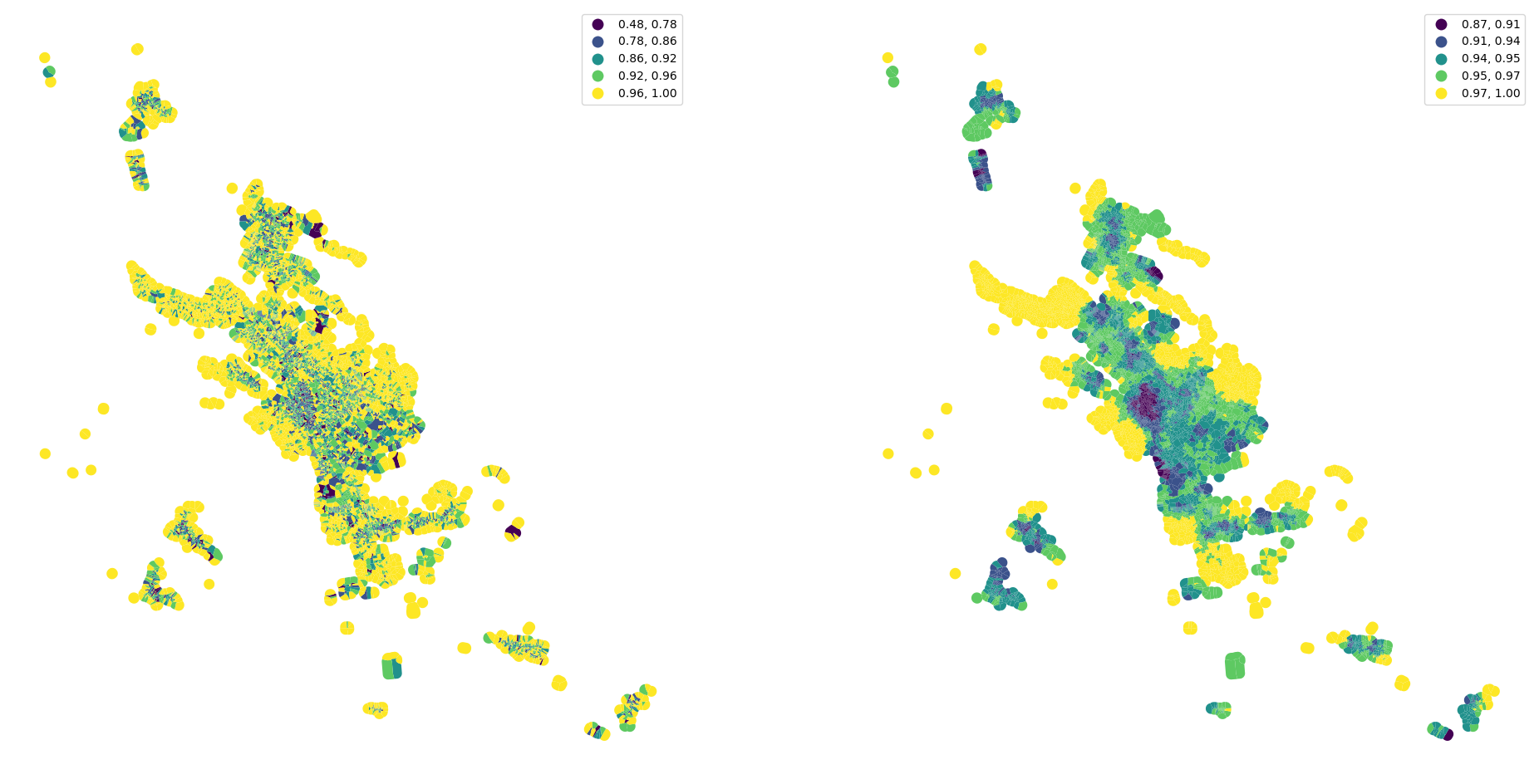
See the difference between original convexity and spatially lagged one.
[37]:
fig, ax = plt.subplots(1, 2, figsize=(24, 12))
tessellation.plot("convexity", ax=ax[0], scheme="natural_breaks", legend=True)
merged.plot(percentiles_joined['convexity_50'].values, ax=ax[1], scheme="natural_breaks", legend=True)
ax[0].set_axis_off()
ax[1].set_axis_off()
Clustering#
Now we can use obtained values within a cluster analysis that should detect types of urban structure.
Standardize values before clustering.
[38]:
standardized = (percentiles_joined - percentiles_joined.mean()) / percentiles_joined.std()
standardized.head()
[38]:
| area_x_25 | area_x_50 | area_x_75 | convexity_25 | convexity_50 | convexity_75 | neighbors_25 | neighbors_50 | neighbors_75 | covered_area_25 | ... | openness_75 | degree_25 | degree_50 | degree_75 | closeness_25 | closeness_50 | closeness_75 | meshedness_25 | meshedness_50 | meshedness_75 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 3.874598 | 3.533443 | 2.323781 | -1.155053 | -2.962302 | -3.777994 | -2.142978 | -2.316295 | -2.359476 | 4.382338 | ... | 1.567482 | 1.157891 | 0.759092 | 0.405637 | 0.271975 | 0.011717 | -0.211542 | 1.432601 | 1.194016 | 0.727337 |
| 1 | 0.832751 | 1.410208 | 1.680435 | 0.651102 | 0.318504 | 0.394242 | -1.533425 | -1.566368 | -1.503667 | 2.688808 | ... | 1.810087 | 0.107411 | 0.759092 | 0.405637 | 0.384216 | 0.113805 | -0.041475 | 1.114745 | 1.194016 | 1.027147 |
| 2 | 2.513958 | 2.401474 | 2.323781 | -1.155053 | -0.141132 | -0.292831 | -2.126994 | -2.257388 | -2.252308 | 2.981910 | ... | 1.567482 | 1.157891 | 0.759092 | 0.405637 | 0.271975 | 0.011717 | -0.211542 | 1.432601 | 1.194016 | 0.727337 |
| 3 | 0.194660 | 0.650176 | 2.327818 | 0.983041 | 1.237615 | 1.189205 | -1.768334 | -1.151946 | -0.779495 | 0.249610 | ... | 0.172577 | -1.468310 | -0.372709 | 1.030416 | -0.390730 | -0.370683 | -0.216644 | 0.843632 | 0.881838 | 0.484633 |
| 4 | 2.958808 | 2.401474 | 2.105787 | -0.720716 | -0.141132 | -0.292831 | -2.087688 | -2.228352 | -2.252308 | 2.886543 | ... | 1.567482 | 1.157891 | 0.759092 | 0.405637 | 0.271975 | 0.011717 | -0.211542 | 1.432601 | 1.194016 | 0.727337 |
5 rows × 60 columns
How many clusters?#
To determine how many clusters we should aim for, we can use a little package called clustergram. See its documentation for details.
[39]:
cgram = Clustergram(range(1, 12), n_init=10, random_state=42)
cgram.fit(standardized.fillna(0))
show(cgram.bokeh())
K=1 skipped. Mean computed from data directly.
K=2 fitted in 0.072 seconds.
K=3 fitted in 0.073 seconds.
K=4 fitted in 0.084 seconds.
K=5 fitted in 0.149 seconds.
K=6 fitted in 0.139 seconds.
K=7 fitted in 0.134 seconds.
K=8 fitted in 0.196 seconds.
K=9 fitted in 0.230 seconds.
K=10 fitted in 0.261 seconds.
K=11 fitted in 0.251 seconds.
Clustegram gives us also the final labels. (Normally, you would run the final clustering on much larger number of initialisations.)
[40]:
cgram.labels.head()
[40]:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 3 | 4 | 1 | 1 | 7 | 6 | 7 | 9 |
| 1 | 0 | 1 | 0 | 3 | 4 | 1 | 1 | 1 | 6 | 7 | 9 |
| 2 | 0 | 1 | 0 | 3 | 4 | 1 | 1 | 7 | 6 | 7 | 9 |
| 3 | 0 | 1 | 0 | 0 | 1 | 2 | 5 | 1 | 3 | 4 | 6 |
| 4 | 0 | 1 | 0 | 3 | 4 | 1 | 1 | 7 | 6 | 7 | 9 |
[41]:
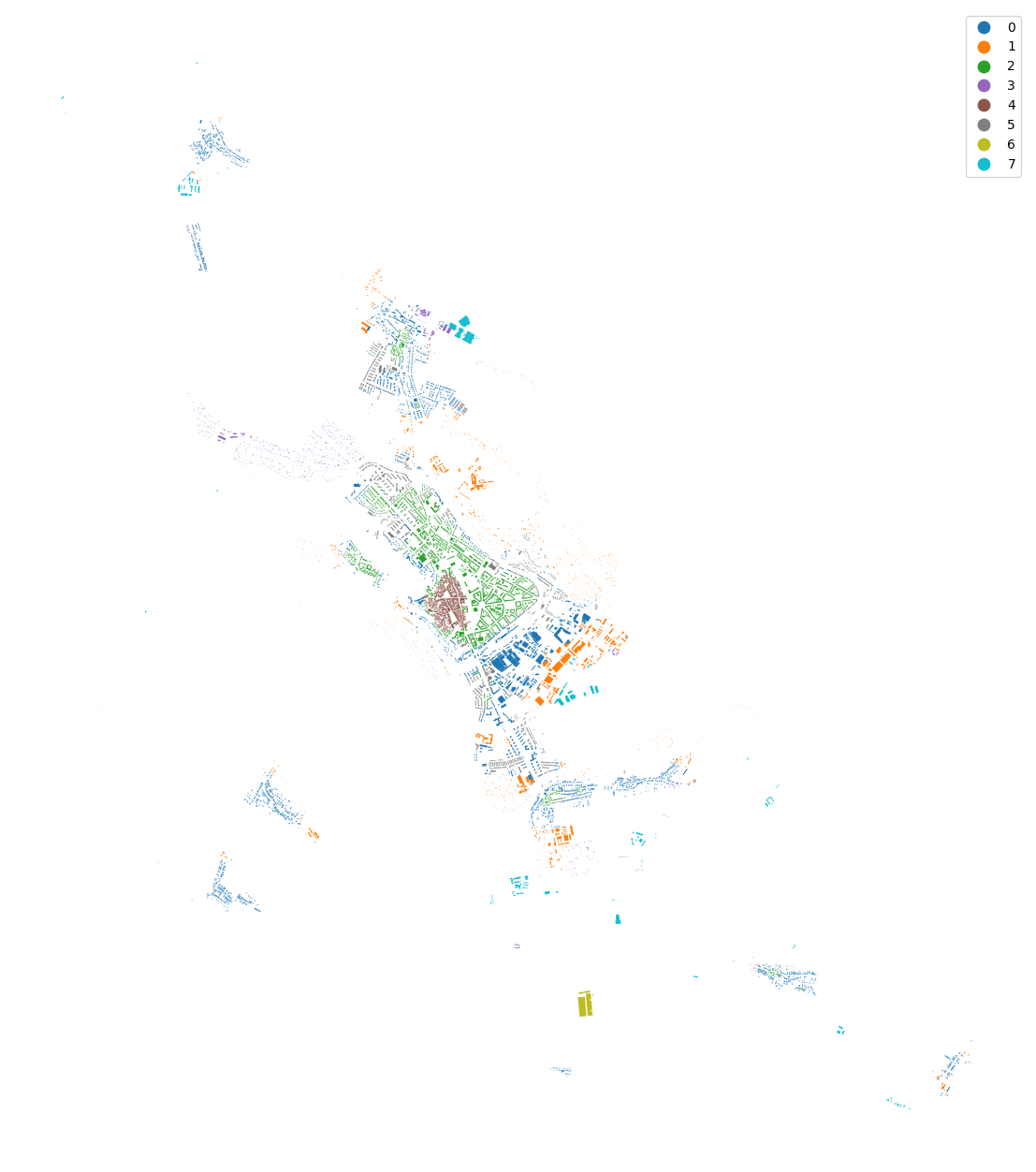
merged["cluster"] = cgram.labels[8].values
urban_types = buildings[["geometry", "uID"]].merge(merged[["uID", "cluster"]], on="uID")
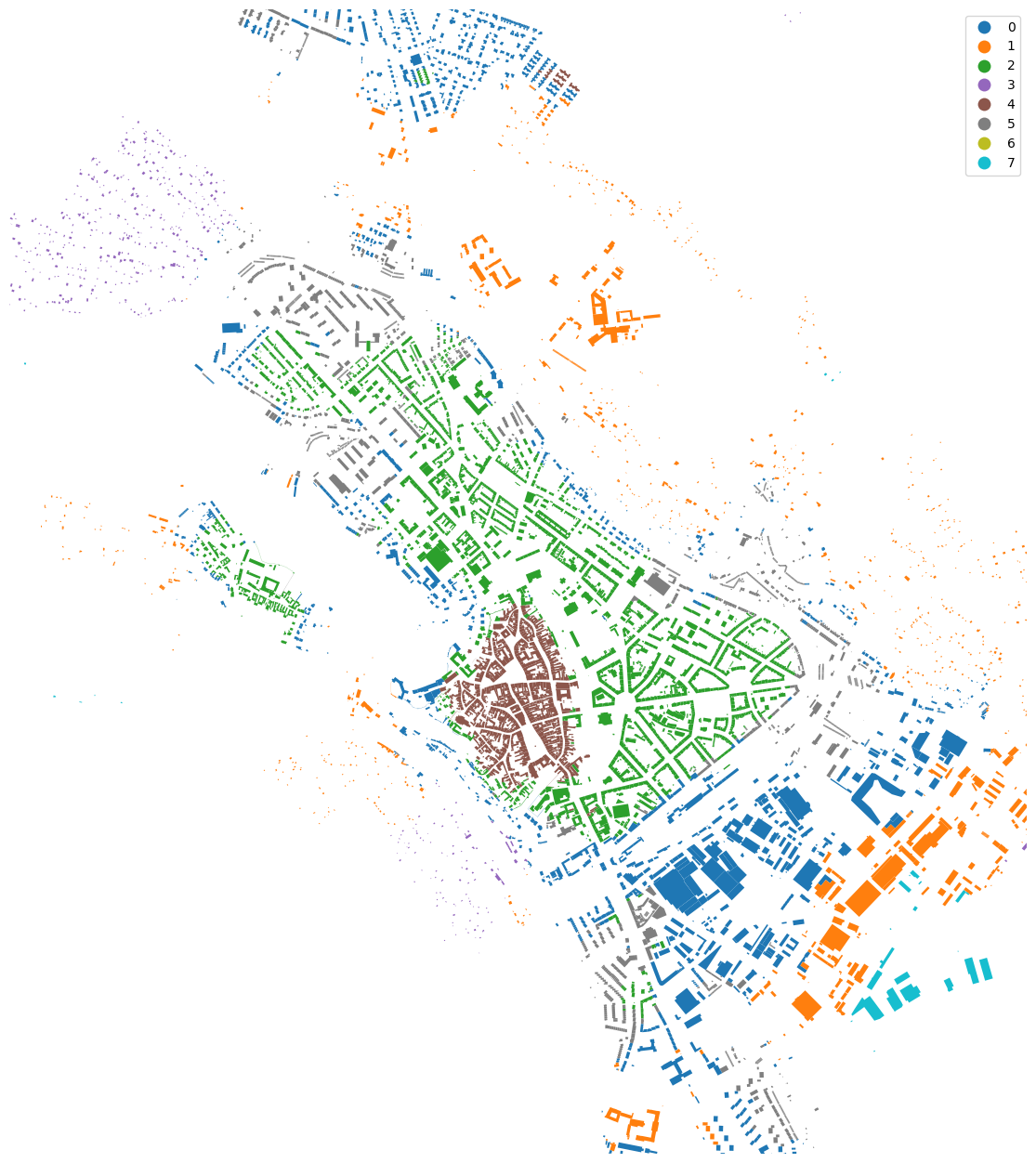
urban_types.plot("cluster", categorical=True, figsize=(16, 16), legend=True).set_axis_off()
[42]:
ax = urban_types.plot("cluster", categorical=True, figsize=(16, 16), legend=True)
ax.set_xlim(-645000, -641000)
ax.set_ylim(-1195500, -1191000)
ax.set_axis_off()